Недавно я тестировал производительность разных компьютеров с помощью простой фортрановской программки. Идея была проверить 1) насколько быстро процессор справляется с суммированием в цикле и 2) точность суммирования. В моем тесте я вычислял S=\sum j по целым числам в интервале [-N,N] при достаточно больших N. Результат нам известен заранее - мы должны иметь S=0 при любом N.
Было интересно проверить насколько быстро и точно компьютер получит 0 прямым суммированием без группировки членов при увеличении N. С помощью этого теста я хотел выбрать оптимальную систему для своих вычислений.
Результаты теста мне показались забавными и, рискну предположить, небезЫнтересными, и я решил изложить их в этой небольшой заметке.
Нас интересует так называемая двойная точность и мы объявим S как 64-битную переменную real*8. Я использовал ``гнутый'' компилятор gfortran и запускал тестовый код на нескольких компьютерах с Linux. На 64-разрядных ОС x86_64 код начинает ошибаться начиная примерно с N = 2**27 ~ 1.3E8. Очевидно, сумма в цикле сначала собирается из членов одного знака и достигает значения S ~ N**2/2 и только после этого к S начинают добавляться члены другого знака.
Какая практическая точность у 64-битной переменной типа real*8?
Казалось бы число значимых цифр 64-битной переменной можно оценить как lg(2**64) ~ 19. Однако, как нас
учит википедия,
на практике точность 64-битной вещественной переменной только около 16 цифр. При N=2**27 старшие значения S в цикле уже не помещаются в эту разрядность, код начинает округлять S, ошибки округления накапливаются, и в результате мы не получаем точного сокращения всех членов.
В статье википедии про двойную точность есть ссылка на формат чисел с расширенной двойной точностью (80-бит). Оказывается, что процессоры x86 и x86-64 поддерживают этот формат на уровне железа. Даже более того, 80-битовый формат вещественных чисел является естественным для мат. сопроцессора (387). Сопроцессор проводит внутренние (промежуточные) вычисления в 80-битовом формате, для уменьшения ошибок округления и повышения точности конечного результата. Если ему подсовывают 64-битную переменную, то он ее преобразовывает в 80-бит, причем делает это дважды: на входе и на выходе.
Компиллятор gfortran поддерживает формат переменных расширенной точности как real*10. Практическая точность этого формата (т.е. число значимых цифр), как мы теперь знаем, отличается от наивной оценки lg(2**80) ~ 24 и близка к lg(2**64), т.е. составляет 18 (если повезет, то 19) знаков.
Мне показалось интересным проверить как формат real*10 будет работать в моей тестовой программе. Для этого достаточно в заголовках задать параметр Prec=10. Как и ожидалось, точность вычислений при этом существенно повышается, код достойно держится до N=2**32, но начинает ошибаться при N=2**33, в соответствии с прикидками данными выше.
Повышение точности кода только за счет смены декларации типа переменных - уже хорошо. Но самым забавным оказалось то, что код с real*10 не только точнее, но и быстрее кода с real*8! Кажется естественным, что при переходе от 64-битным к 80-битным переменным не должно быть лишних преобразований переменных при общении с мат. сопроцессором. Видимо в этом - причина ускорения кода. Но неожиданным оказалось ускорение работы программы в 2 раза для Intel Xeon на нашем кластере!
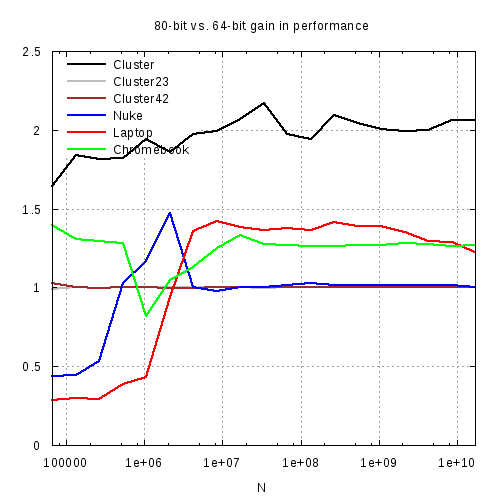
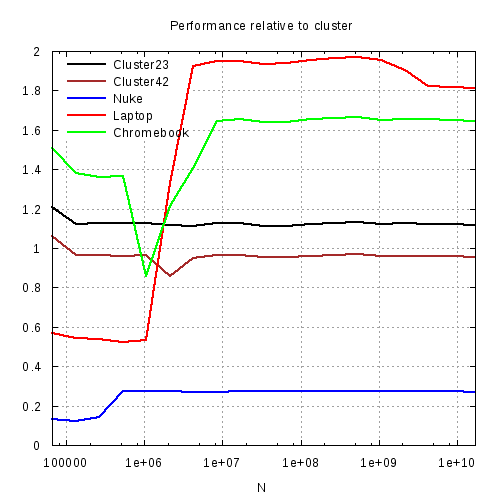
Для количественной иллюстрации эффекта я нарисовал пару графиков:
1) относительное изменение производительности компьютера при переходе от 64-битных переменных типа real*8 к 80-битным переменным типа real*10
2) производительность разных систем относительно машины cluster.
Под производительностью понимается обратное время вычисления суммы х.
Почти все машины были с 64-битной версией Linux, кроме nuke, на котором установлен 32-битный Debian (см. таблицу).
Оказалось, что код на cluster работает в 2 раза быстрее с 80-битными переменными! Как видно из графика, существенное ускорение 80-битного кода характерно для 64-битных процессоров Intel. Для AMD (и 32-битной системы на nuke) не наблюдается существенного выигрыша в производительности от перехода от 64- к 80-битной переменной (но точность вычислений повышается).
Тестируемые компьютеры:
_______________________________________________________________________________________ System CPU N.cores Linux kernel gfortran _______________________________________________________________________________________ cluster Intel Xeon 3.0GHz 4 SL x86_64 2.6.32-... 4.5.2 cluster23 AMD Opteron 8214 8 SL x86_64 2.6.18-... 4.1.2 cluster31 Intel Xeon E5530 2.4GHz 8 SL x86_64 2.6.18-... 4.1.2 cluster42 AMD Opteron 6168 1.9GHz 24 SL x86_64 2.6.32-... 4.4.6 nuke Intel Pentium E5400 2.7GHz 2 Debian i686 3.2.0-4 4.7.2 laptop Intel i5-2410M 2.30GHz 4 Debian x86_64 3.2.0-4 4.7.2 chromebook Intel Celeron N2840 2.16GHz 2 Debian x86_64 3.10.18 4.9.2 _______________________________________________________________________________________
 |
 |
Время вычисления S(N) растет пропорционально N. При этом, как видно из графика, даже скромные, но более новые системы работают быстрее кластерных узлов. Мне показалось забавным и показательным, что мой новый хромбук, который, казалось бы, и претендовать на вычислительную производительность не может, оказался в этом тесте быстрее процессора сервера cluster. Однако, в поддержку х-бука отмечу, что это полностью 64-битная система с хоть и кастрированным (мобильным), но новым 64-битным процессором и со свежим gfortran v.4.9 компилятором. Можно предположить, что этот компилятор оптимизирует код лучше, чем старые компиляторы кластерных машин. Тем не менее, причины того, что Intel Celeron N2840 2.58GHz (в турбо режиме) на 60% быстрее Intel Xeon 3.0GHz все еще кажутся мне загадочными. В этом контексте, было бы интересно протестировать вычислительные возможности процессоров ARM, которые стоят в большинстве планшетов и телефонов. Может быть уже пора попытаться использовать телефоны не только по их прямому назначению :-?)
Очевидно, что производительность кода зависит не только от процессора, но и от компилятора и от параметров компилирования. Графики нарисованы для результатов компиляции с флагом оптимизации O2 и могут выглядеть по-другому с другими флагами gfortran
(я не изучал другие компиляторы).
Флагов у gfortran много и изучение их возможностей на предмет оптимизации может легко занять все имеющееся время. Я только отмечу флаг
-march, который учитывает архитектуру процессора. Желающие могут попробовать оптимизировать код под конкретную машину с помощью параметра -march=native.
Показательным в этом смысле оказался пример машины nuke, на которой установлен Debian 32-бит. Машина nuke была самой медленной в тестах со стандартной оптимизацией O2, хотя частоты процессоров у nuke и cluster сравнимы. Первым впечатлением было, что здесь сказывается разрядность ОС. Однако, использование флага -march=native оказалось весьма эффективным и производительность моего тестового кода на 32-битном ядре Linux (процессор у nuke 64-битный) оказалась сравнимой с производительностью "полностью" 64-битного cluster.
Описанные выше тесты проводились на одном ядре процессора. Важно также проверить, что мы выиграем (ли) в производительности и точности кода с 80-битными переменными при попытке распараллелить программу.
Для этого я использовал OpenMP, который поддерживается даже на самых старых версиях компиляторов на кластере.
В моем тестовом коде параллельность управляется параметром prl: prl=0 приводит к последовательному коду для одного процессора, а prl=1 включает параллельные вычисления на всех доступных процессорных ядрах.
Код с одним циклом очень эффективно распараллеливается средствами OpenMP. Я его тестировал на нескольких системах, результаты для производительности кода суммированы на графике.
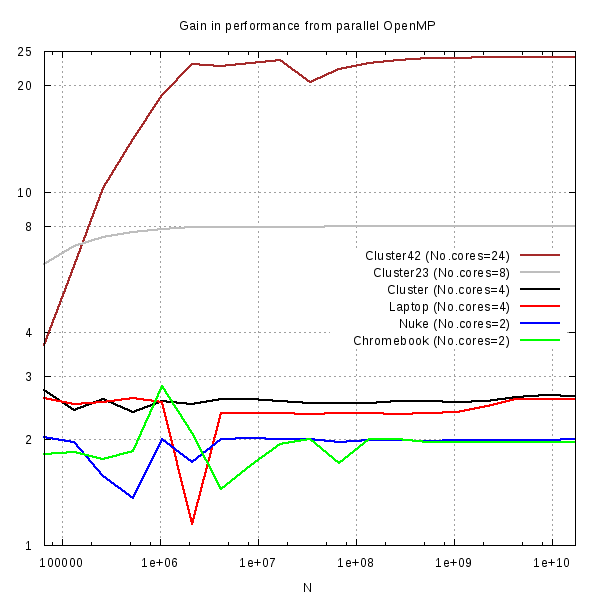
Эффект параллельности впечатляет, производительность при достаточно больших N увеличивается пропорционально числу задействованных ядер (исключение составили 4х ядерные системы)!
Параллельное выполнение суммирования в цикле также благоприятно сказывается на точности сокращения членов разного знака при больших N.
Вот результаты для S(N) для 64-битной и 80-битной версий распараллеленых с помощью OpenMP для разного количества процессоров:
64-bit version: p N=2**p S No.cores=1 S No.cores=2 S No.cores=4 S No.cores=8 S No.cores=24 26 67108864 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 27 134217728 -11585.0000000 -5792.00000000 0.00000000000 0.00000000000 0.00000000000 28 268435456 -232471923.000 -183344816.000 -88438552.0000 -42486318.0000 1.00000000000 29 536870912 -519822953.000 -461237984.000 -427413984.000 -310103436.000 -137253444.000 30 1073741824 -1065319903.00 -1002421120.00 -985636384.000 -940626304.000 -738108400.000 31 2147483648 -2143284860.00 -2078265344.00 -2069877248.00 -2047507168.00 -1923873512.00 32 4294967296 -4292867744.00 -4226779136.00 -4222556160.00 -4211342720.00 -4150743808.00 33 8589934592 -8588876000.00 -8519720960.00 -8518819840.00 -8513936384.00 -8484304896.00 34 17179869184 -17179339772.0 -17062330368.0 -17075896320.0 -17095215104.0 -17092972544.0 80-bit version: p N=2**p S No.cores=1 S No.cores=2 S No.cores=4 S No.cores=8 S No.cores=24 26 67108864 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 27 134217728 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 28 268435456 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 29 536870912 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 30 1073741824 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 31 2147483648 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 32 4294967296 0.00000000000 0.00000000000 0.00000000000 0.00000000000 0.00000000000 33 8589934592 -6074000997.00 -4294967292.00 -1464933360.00 0.00000000000 0.00000000000 34 17179869184 -16070296103.0 -13588082112.0 -11364843456.0 -7094119694.00 -591823493.000
Как видно, выполнение параллельного кода на 24 ядрах позволяет добиться "почти" точного результата для 64-битной версии для N=2**28 ~ 2.7E8 (сравниваем с N~0.7E8 для 1 ядра). Это связано, по-видимому, с тем что в парциальных суммах, которые выполняются параллельно, накапливается меньше ошибок округления из-за уменьшения количества членов в сумме и ее абсолютной величины. Для 80-битной версии результаты выглядят еще оптимистичнее. Как уже отмечалось выше, точный результат получается для N=2**32 уже на 1 ядре. На 8 ядрах мы имеем точное сокращение для N=2**33.
Сравнение времен затраченных на вычисление S приводит к картине похожей на результаты на 1 процессоре. Процессоры Intel(64-bit) работают быстрее с 80-битной версией кода (для Intel Xeon сервера cluster имеем выигрыш в 2 раза), тогда как производительность AMD довольно безразлична к разрядности S. Но в любом случае точность вычислений существенно повышается.
Комментарий: исходные коды и скрипты можно найти здесь.
© С. Кулагин, ИЯИ ОТФ